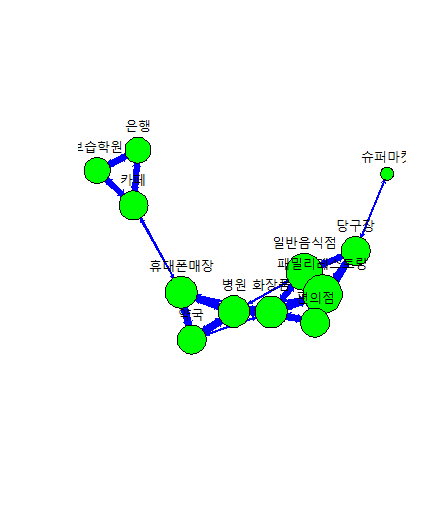
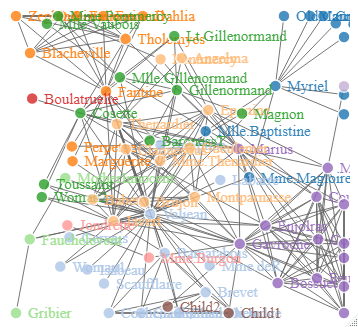
레미제라블 3D 인물 네트워크
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
# 3D 시각화 패키지 설치
install.packages("networkD3")
install.packages("dplyr")
library(networkD3)
library(dplyr)
# data set 소설 레미제라블 인물 관계도
# 데이터 로드
data(MisLinks, MisNodes)
head(MisNodes) # size : 몇번 언급되었는지에 대한 정보
head(MisLinks) # value : 인물끼리 몇번 만났는지 데이터
# plot
D3_network_LM<-forceNetwork(Links = MisLinks, Nodes = MisNodes,
Source = 'source', Target = 'target',
NodeID = 'name', Group = 'group',opacityNoHover = TRUE,
zoom = TRUE, bounded = TRUE,
fontSize = 15,
linkDistance = 75,
opacity = 0.9)
D3_network_LM
|
cs |
모바일관련 소송 시각화
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
|
# IT 회사들간 법적 소송관계도 시각화
# 데이터 로드
links = '[
{"source": "Microsoft", "target": "Amazon", "type": "licensing"},
{"source": "Microsoft", "target": "HTC", "type": "licensing"},
{"source": "Samsung", "target": "Apple", "type": "suit"},
{"source": "Motorola", "target": "Apple", "type": "suit"},
{"source": "Nokia", "target": "Apple", "type": "resolved"},
{"source": "HTC", "target": "Apple", "type": "suit"},
{"source": "Kodak", "target": "Apple", "type": "suit"},
{"source": "Microsoft", "target": "Barnes & Noble", "type": "suit"},
{"source": "Microsoft", "target": "Foxconn", "type": "suit"},
{"source": "Oracle", "target": "Google", "type": "suit"},
{"source": "Apple", "target": "HTC", "type": "suit"},
{"source": "Microsoft", "target": "Inventec", "type": "suit"},
{"source": "Samsung", "target": "Kodak", "type": "resolved"},
{"source": "LG", "target": "Kodak", "type": "resolved"},
{"source": "RIM", "target": "Kodak", "type": "suit"},
{"source": "Sony", "target": "LG", "type": "suit"},
{"source": "Kodak", "target": "LG", "type": "resolved"},
{"source": "Apple", "target": "Nokia", "type": "resolved"},
{"source": "Qualcomm", "target": "Nokia", "type": "resolved"},
{"source": "Apple", "target": "Motorola", "type": "suit"},
{"source": "Microsoft", "target": "Motorola", "type": "suit"},
{"source": "Motorola", "target": "Microsoft", "type": "suit"},
{"source": "Huawei", "target": "ZTE", "type": "suit"},
{"source": "Ericsson", "target": "ZTE", "type": "suit"},
{"source": "Kodak", "target": "Samsung", "type": "resolved"},
{"source": "Apple", "target": "Samsung", "type": "suit"},
{"source": "Kodak", "target": "RIM", "type": "suit"},
{"source": "Nokia", "target": "Qualcomm", "type": "suit"}
]'
link_df = jsonlite::fromJSON(links)
# node의 index 숫자는 0부터 시작
# dplyr::row_number()가 1부터 숫자를 매기기 때문에 1씩 뺌
node_df = data.frame(node = unique(c(link_df$source, link_df$target))) %>%
mutate(idx = row_number()-1)
# node_df에서 index값을 가져와서 source와 target에 해당하는 index 값을 저장
link_df = link_df %>%
left_join(node_df %>% rename(source_idx = idx), by=c('source' = 'node')) %>%
left_join(node_df %>% rename(target_idx = idx), by=c('target' = 'node'))
# 데이터 확인
node_df
link_df
# 3D 시각화 패키지 설치
library(networkD3)
library(dplyr)
# plot
D3_network_LM<-forceNetwork(Links = link_df,
Nodes = node_df,
Source = 'source_idx', Target = 'target_idx',
NodeID = 'node', Group = 'idx',
opacityNoHover = TRUE, zoom = TRUE,
bounded = TRUE,
fontSize = 15,
linkDistance = 75,
opacity = 0.9)
D3_network_LM
|
cs |

'인공지능 > 실습예제' 카테고리의 다른 글
| (R) k-means 활용하기 2 - 성적으로 학생 군집화 (0) | 2020.07.03 |
|---|---|
| (R) k-means 활용하기 1 - R로 k-means 시각화 / 패키지 사용 (0) | 2020.07.03 |
| (R) 연관규칙(Apriori) 활용하기 2 - 독서시간과 사람을 만난 횟수의 연관성 (0) | 2020.07.02 |
| (R) 연관규칙(Apriori) 활용하기 1 - 업종별 연관성 (0) | 2020.07.02 |
| (R) 연관규칙(Apriori) 이해하기 (0) | 2020.07.02 |