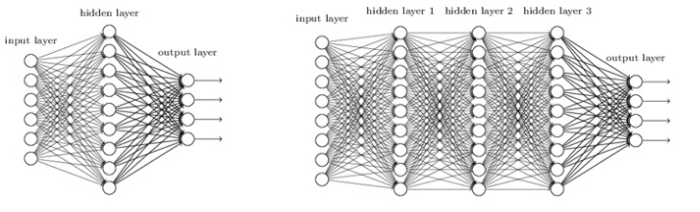
앞서 신경망을 구성하기 위해서 활성화 함수, 가중치 등이 필요하다는 것을 설명했다. 위의 그림은 인공 신경망이다. 왼쪽의 그림은 은닉층이 1개이고 오른쪽 그림은 은닉층이 3개이다. 위의 선만 봐도 알 수 있다시피 신경망은 깊이가 깊어질수록, 은닉층의 노드 수가 많으면 많을수록 계산이 복잡해진다. 하지만 우리는 데이터 한 두개를 학습시키는 것이 아니라 수천, 수만개의 데이터를 학습시킨다. 우리는 인간이 할 수 있는 일이지만 더 정확하면서도 빠르게 예측, 분류하기 위해 인공지능을 사용하고자 한다. 어떻게 해야 수많은 은닉층을 가진 신경망도 빠르게 데이터를 학습시킬 수 있을까?
배치(Batch)
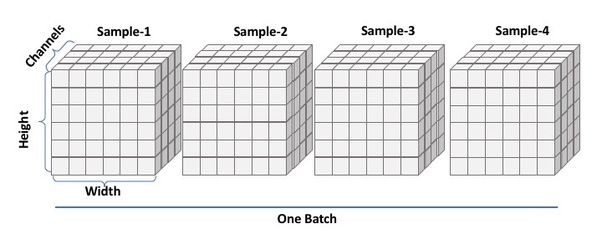
우리는 인공신경망에 10만개의 데이터를 학습시키고자 한다. 이 10만개의 데이터를 어떻게 해야 빠르게 학습시킬 수 있을까? 컴퓨터의 핵심인 CPU는 결국에는 계산이 주요한 능력이기 때문에 계산이 매우 빠르다. 따라서 우리는 데이터를 1개씩 입력받아 총 10만번의 연산을 진행하는 것보다 한번에 큰 묶음으로 데이터로 입력받아(Batch) n번의 연산을 진행하는 것이 더 빠르다. 즉, 느린 I/O를 통해 데이터를 읽는 횟수를 줄이고 CPU나 GPU로 순수 계산을 하는 비율을 높여 속도를 빠르게 할 수 있다는 뜻이다. 또한 수치 계산 라이브러리 대부분이 큰 배열을 효율적으로 처리할 수 있도록 고도로 최적화되어 있기 때문에 Batch(묶음)로 데이터를 입력받아 학습시키는 것이 속도 측면에서 효율적이다.
그렇다면 미니배치 학습이라는 것은 무엇일까?
미니배치 (Mini-Batch)
미니배치를 설명하기에 앞서 데이터를 하나씩 학습시키는 방법과 전체를 학습시키는 방법의 장단점에 대해 소개하겠다.
데이터를 하나 하나씩 신경망에 넣어 학습을 시키면 우선 장점으로는 신경망을 한번 학습시키는데 소요되는 시간이 매우 짧다는 것이다. 하지만 데이터를 하나씩 입력받으면 계산 속도가 사실상 늦어진다. 우리는 대부분 딥러닝에 GPU를 많이 사용하는데 그 이유가 GPU의 병렬처리에 있다. 하지만 데이터를 한개씩 넣어 인공지능을 학습시키면 사실상 GPU의 병렬처리를 사용하지 않으니 그만큼 자원 낭비가 된다. 또한 오차를 줄이기 위해 사용하는 Loss Function에서 최적의 파라미터를 설정하는데 상당히 많이 헤매게 된다.
전체 데이터를 입력하는 경우는 한번에 여러개의 데이터에 대해서 신경망을 학습시킬 수 있으므로 오차를 줄일 수 있는 cost function의 최적의 parameter를 하나씩 학습하는것보다 빠르게 알아낼 수 있다. 하지만 전체 데이터를 학습시키기 때문에 신경망을 한 번 학습시키는데 소요되는 시간이 매우 길다.
위의 문제점과 장점을 적절히 섞은 것이 바로 미니 배치이다. 미니 배치는 SGD(Stochastic Gradient Descent : 확률적 경사 하강법)와 배치를 섞은 것으로 전체 데이터를 N등분하여 각각의 학습 데이터를 배치 방식으로 학습시킨다. 따라서 최대한 신경망을 한 번 학습시키는데(iteration) 걸리는 시간을 줄이면서 전체 데이터를 반영할 수 있게되며 효율적으로 CPU와 GPU를 활용할 수 있게 된다.
에폭 (Epoch)
Epoch는 인공 신경망에서 전체 데이터 셋에 대해 한 번 학습을 완료한 상태를 의미한다. 신경망은 최적의 가중치와 기타 파라미터를 찾기 위해서 역전파 알고리즘(backpropagation algorithm)을 사용한다. 역전파에는 파라미터를 사용하여 입력부터 출력까지의 각 계층의 weight을 계산하는 과정인 순방향과 반대로 거슬러 올라가며 다시 한 번 계산 과정을 거쳐 기존의 weight을 수정하는 역방향으로 나뉜다. 이 순방향과 역방향을 모두 완료하면 한 번의 Epoch가 완료됨을 의미한다. 더 쉽게 말하자면 1에폭은 학습에서 훈련 데이터를 모두 소진했을 때의 횟수에 해당한다.
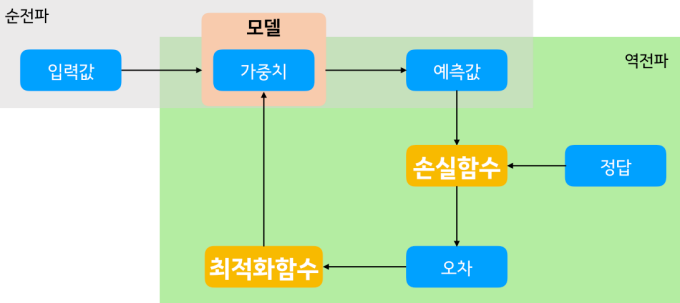
위의 그림에서 손실함수라는 것은 Loss Function, 즉 Cost Function을 의미한다.
예를 들어 훈련 데이터 10000개를 100개의 미니배치로 학습할 경우, 최적의 가중치를 구하기 위해 SGD를 100번 반복해야 모든 훈련 데이터를 학습에 활용하기 때문에 100회가 1에폭이 된다.
위의 그림의 손실함수(Loss Function)에 대해 더 자세히 설명하자면 손실함수란 Loss Function, 혹은 Cost Function이라고도 하며, 신경망에서 내놓는 결과값과 실제 결과값 사이의 차이를 정의하는 함수이다. 우리는 이 손실함수의 값이 최소값이어야 가장 좋은 신경망을 만들었다고 할 수 있다. 가장 많이 쓰는 손실 함수로 오차 제곱합(Sum of Sqaures for Error)와 교차 엔트로피 오차(Cross Entropy Error)가 있으며, 오차 제곱 합은 회귀에 주로 사용하고, 교차 엔트로피 오차는 분류에 주로 사용한다.
그리고 필자는 처음에 미니배치를 공부할 때 수만건의 데이터 중에서 n개만큼의 데이터를 임의로 추출하기 때문에 당연히 복원 추출이라고 생각했는데 (왜냐하면 데이터 개수가 매우 많으면서 데이터 전체를 표현해야하기 때문에), Epoch의 개념에서는 전체 데이터셋을 사용해야 1Epoch가 된다는 것을 읽으며 골머리를 앓았다.
배치, 혹은 미니배치학습을 할 때 배치는 복원 추출인가? 비복원 추출인가?
이에 대한 해답을 정확히 알 수는 없었으나, 어쨌든 복원 추출이나 비복원 추출이나 사실상 크게 다르지 않다는게 결론이다. 이에 대한 이유는 데이터가 매우 많기 때문이다. 수많은 데이터 중에서 임의의 개수로 임의의 데이터를 추출하는 것을 n번 반복하면 사실상 비복원 추출이나 복원 추출이나 전체 데이터셋을 사용한다고 볼 수 있기 때문이다.
확률적 경사 하강법 (SGD : Stochastic Gradient Descent)
SGD는 신경망을 학습할 때마다 가중치를 갱신한다. 기존의 경사 하강법과 개념이 다르지 않은데, 확률적이라는 말이 앞에 붙은 이유는 학습할 때마다 가중치를 갱신하기 때문에 학습할 때마다 신경망의 성능이 들쑥날쑥 변하면서 정답에 가까워지기 때문에 '무작위적'으로 보이기 때문이다.
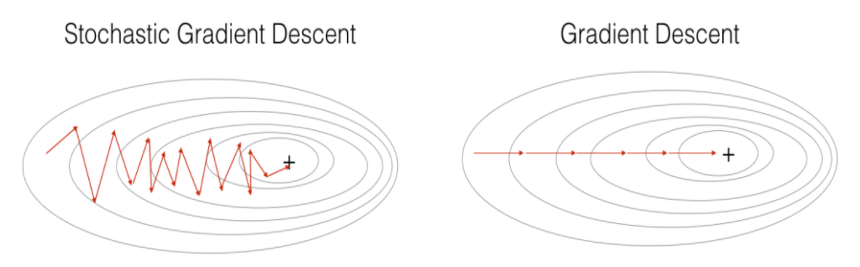
SGD이외에도 배치에 대한 자세한 설명과 BGD에 대해 알고 싶다면 블로그를 참고하길 바란다.
'인공지능 > 인공지능 이론' 카테고리의 다른 글
| 18. 다양한 최적화 알고리즘 (0) | 2020.08.06 |
|---|---|
| 17. 오차 역전파 (Backpropagation) (1) | 2020.08.05 |
| 15. 항등함수와 Softmax 함수 (2) | 2020.08.03 |
| 14. 다층퍼셉트론 / Sigmoid / ReLU (0) | 2020.07.01 |
| 13. Perceptron (퍼셉트론) (0) | 2019.09.14 |