다층퍼셉트론
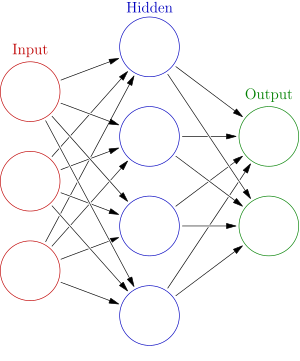
위의 이미지를 보자. 앞에서 설명했던 기본적인 퍼셉트론이 여러개의 층으로 이루어지는 것을 다층 퍼셉트론이라고 한다. Input은 입력층, Hidden은 은닉층, Output은 출력층으로 표현한다. 여기서 은닉층(Hidden)이 여러개를 갖게 되는 것을 다층 퍼셉트론이라고 할 수 있다.
model = Sequential()
model.add(Dense(12, input_dim=8, activation='relu'))
model.add(Dense(8, activation='relu'))
model.add(Dense(1, activation='sigmoid'))
위의 코드는 다층퍼셉트론을 만드는 기본적인 코드이다. 그런데 저 코드에서 activation에 있는 relu와 sigmoid는 도대체 뭘까? 우리는 이것들을 활성화 함수라고 한다.
활성화 함수
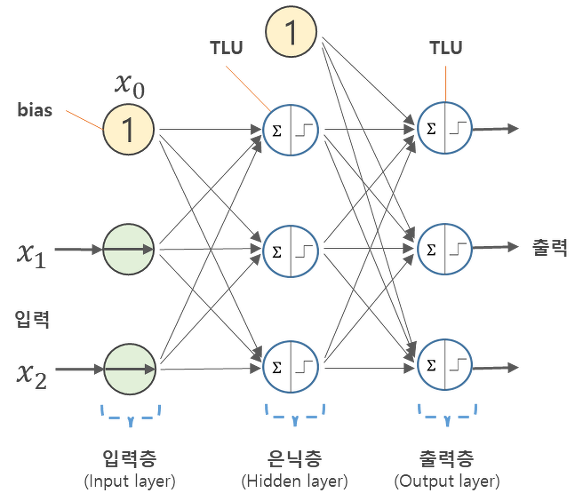
위의 그림은 신경망을 나타내는 그림이다. 여기서 활성화 함수에 해당하는 것은 계단함수이다. 계단함수라는 것은 특정 임계값을 넘기면 활성화되는, 즉 0과 1로 출력되는 함수를 의미한다.
import matplotlib.pylab as plt
import numpy as np
def step_function(x) :
result = x > 0
return result.astype(np.int)
x = np.arange(-5,5,0.1)
y = step_function(x)
plt.plot(x,y)
plt.ylim(-0.1,1.1)
plt.show()
하지만 단층퍼셉트론이 아니라 다층퍼셉트론 같은 경우는 활성화 함수로 계단함수를 쓸 수 있을까? 어떤 기준으로 0과 1을 나눠야 하는걸까? 그것에 대한 해답이 sigmoid와 relu이다.
Sigmoid
import matplotlib.pylab as plt
import numpy as np
def sigmoid(x) :
return 1/(1+np.exp(-x))
x = np.array([-1,1,2])
sigmoid(x)
x = np.arange(-5,5,0.1)
y = sigmoid(x)
plt.plot(x,y)
plt.ylim(-0.1,1.1)
plt.show()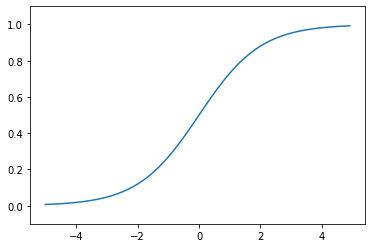
위의 그래프에 대해서는 내가 이전에 맥락을 풀어 설명했으니 참고하길 바란다. 하지만 귀찮은 사람들을 위해 간략하게 말하자면 그래프 그대로 데이터를 0과 1로 분류한다는 뜻이다. 이것이 Sigmoid 함수이다. 앞서 말했지만 퍼셉트론은 인간의 뉴런을 모델로 했기 때문에 다층 퍼셉트론같은 경우 데이터를 0과 1로 구분하여 역치 이상(1)일 경우 데이터를 다음 퍼셉트론으로 넘기는 방식으로 운영되어진다. 그런데 이쯤 되면 궁금증이 생긴다. 계단함수나 Sigmoid나 둘 다 0 또는 1 혹은 0~1 사이의 값으로 데이터를 변환해준다는 것이다. 그런데 왜 단층퍼셉트론에는 계단함수를 쓰고 다층퍼셉트론에서는 Sigmoid 또는 ReLU를 사용하는 것일까?
다층 퍼셉트론은 여러개의 은닉층을 보유하고 앞에서 가공되어진 데이터들이 다음 은닉층으로 넘어가는 구조이다. 계단함수를 다층 퍼셉트론에서 사용한다면 우리는 이전 데이터를 오직 0과 1, 즉 극단적인 형태로밖에 받을 수 없고 이런식이라면 다층 퍼셉트론을 만들어 좋은 모델을 만들 수 없게 된다. 하지만 Sigmoid 함수같은 경우는 값을 0~1 사이로 만들어주기 때문에 가공된 데이터를 다음 은닉층으로 보내줘도 극단적인 형태가 아니고 신경망이 데이터를 섬세하게 분류할 수 있도록 도와준다.
좋다. 계단함수보다 Sigmoid를 사용하는 이유를 이제는 충분히 이해했다. 그런데 ReLU는 또 왜 필요한걸까?
ReLU
import matplotlib.pylab as plt
import numpy as np
def relu(x) :
return np.maximum(0,x)
x = np.arange(-5,5,0.1)
y = relu(x)
plt.plot(x,y)
plt.ylim(-0.5,5.5,0.1)
plt.show()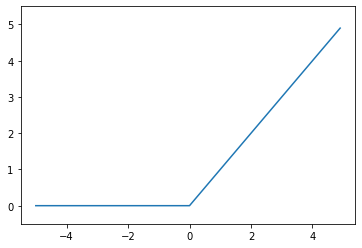
ReLU함수는 Sigmoid의 단점을 해결하기 위해 나왔다. Sigmoid 함수의 단점은 0과 1사이의 데이터로 이루어져 있어 역전파를 할수록, 즉 층이 깊어질수록 활성화 값들이 0과 1에 치우쳐져 있어 미분값이 0에 가까워진다는 것이다. 이것을 Vanishing Gradient Problem(기울기 값이 사라지는 문제)이라고 한다. 즉, 전파가 역전파될 때 기울기 소실로 인해서 앞층까지 전파가 안된다는 이야기다. 따라서 이와 같은 문제점을 해결하고자 ReLU 함수를 사용하게 된 것이다.
ReLU는 0보다 작은 값에 대해서는 0을 반환하고, 0보다 큰 값에 대해서는 그 값을 그대로 반환하여 층이 깊어져도 0으로 수렴하는 오류를 범하지 않게 된다.
더 자세한 내용은 블로그를 참고하길 바란다.
+
Leaky ReLU
def leaky_relu(x) :
return np.maximum(0.01*x,x)
x = np.arange(-20,5,0.1)
y = leaky_relu(x)
plt.plot(x,y)
plt.grid()
plt.ylim(-0.5,5.5,0.1)
plt.show()
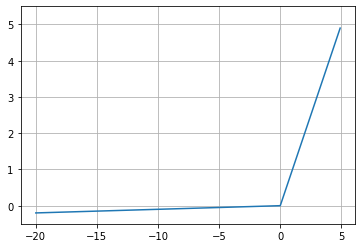
ReLU와 동일하나 x가 음수일때 기울기(gradient)가 0.01이다.
ELU (Exponential Linear Units)
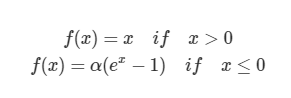
ELU 또한 ReLU와 비슷하나 기울기가 살아남는다는 특징이 있다.
'인공지능 > 인공지능 이론' 카테고리의 다른 글
| 16. 배치(Batch), 미니배치 학습, 에폭(Epoch), SGD (3) | 2020.08.04 |
|---|---|
| 15. 항등함수와 Softmax 함수 (2) | 2020.08.03 |
| 13. Perceptron (퍼셉트론) (0) | 2019.09.14 |
| 12. Clustering (0) | 2019.09.13 |
| 11. 차원의 저주 / PCA (0) | 2019.09.13 |