Regression(회귀)이 결과값을 추정하는 방식이었다면, Classification(분류)은 카테고리에 분류하는 방식이다.
Classification에서 Linear Regression은 사용할 수 없다. 왜냐하면 Classification은 0 또는 1값만 가지는데, linear regression은 그 범위 이상의 값을 가질 수 있기 때문이다. 따라서 Linear Regression을 Classification에서 사용하기 위해서는 0 또는 1 사이의 값만 내보내는 Hypothesis 함수가 필요하다.

위의 그림에서 왼쪽에 위치한 선형 회귀의 그래프를 보자. 그래프의 y축은 -4 ~ 4 까지 분포되어 있는 것을 알 수 있다. 이런 경우는 앞서 공부했던 Regression으로는 풀리지만 0과 1만을 나타내는 Classification에서는 적용되지 못한다. 왜냐하면 y값이 선형적인 값으로 -4 ~ 4 까지 분포하고 있으니까 말이다. 이런 Regression의 한계점을 해결하여 Classification에서도 문제를 풀기 위해서 우리는 Logistic Regression을 사용한다. (똑똑한 인간들 덕에 이만큼 발달된 사회에서 산다지만 내가 밥 벌어먹으려고 공부하다보니 드는 생각은 똑똑한 것들 다 없어졌으면) 오른쪽 그래프를 보자. Logistic Regression은 y값이 0 ~ 1 까지 밖에 없다. 그 사이에 있는 값들은 일정한 기준을 통해 0 또는 1로 구분할 수 있을 것이고 그렇게 되면 우리는 Regression을 Classification에 적용하여 풀 수 있게 될 것이다.
Linear Regression을 Logistic Regression으로 바꿔주기 위해 우리는 Sigmoid Function을 사용한다.

𝑃(𝑦=1|𝑥;𝜃) +𝑃(𝑦=0|𝑥;𝜃) = 1
여기서 만들어진 함수는 1번 class일 확률과 0번 class 일 확률의 합이 항상 1이 되어야 한다.
Cost Function (비용 함수)
우리는 Linear Regression을 Classification에서도 활용하도록 Sigmoid Function을 사용하여 Logistic Regression으로 바꿨다. 그렇기 때문에 우리가 예측한 데이터가 실제 데이터와 얼마나 유사한지에 대해 판단하는 Cost Function 식도 바꿔야 한다. 왜 바꿔야할까? 귀찮아죽겠는데
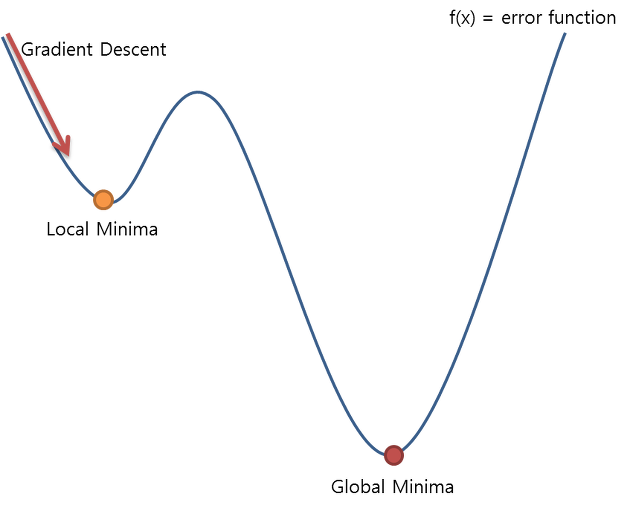
기존의 Linear Regression의 Cost Function을 Logistic Regression에 사용하는 경우는 위의 이미지와 같은 문제가 발생한다.
(Local Minima(모델과 데이터에 따라 경사도가 0인 지점이 여러 개 존재할 수 있는 문제)가 생기는 문제)
왜 Local Minima가 생길까? 그 이유는 로지스틱 회귀에서 사용하는 sigmoid가 비선형 함수이기 때문에 Non-convex Function이 되기 때문이다.
위의 그림에서 볼 수 있다시피 가장 최소값 이전에 구간의 최소값이 존재하므로 우리의 멍청한 컴퓨터는 가장 최소값(Global Minima)을 찾기도 전의 최소값(Local Minima)을 그 함수의 가장 최소값으로 판단할 것이다. 따라서 기존의 Cost Function은 모델의 정확성을 판단하는데 어려움이 있다.


Logistic Regression의 Cost Function은 위와 같다. 빨간색 선은 y=0, 즉 실제 데이터가 0일 때의 그래프이다. x축인 h(x)는 Logistic Regression을 통해 우리가 예측한 값으로 예측값인 h(x)가 실제 데이터의 값인 0과 일치하면 Cost는 0이고, 그와 반대로 예측값을 1로 잘못 예측할 경우 Cost가 기하급수적으로 증가한다. 이는 잘못 예측한 값에 대해 패널티를 주는 개념으로 모델의 예측 정도를 판단하는데 도움이 된다. 파란색 선은 y=1, 즉 실제 데이터가 1일 때의 그래프이고 위의 설명과 같게 예측값과 실제 값이 모두 일치하는 1일 경우에는 Cost가 0, 잘못 예측했을 때는 큰 Cost를 주어 모델이 잘못 예측되었음의 지표를 알려주게 된다. 따라서 Logistic Regression의 Cost Function은 모두 convex하다.
Logistic Regression의 경사하강법

Gradient Descent에 대해서는 앞에서 공부한 Regression에서 자세히 설명하였으므로 여기서는 수식에 대해서만 적겠다. 어쨌든 Logical Regression도 경사하강법(Gradient Descent)을 사용하여 Cost를 최소화하는 계수를 찾는다는 것이다.
단순히 위의 Logistic Regression과 같은 그래프 모양이 나타난다면 우리는 대부분 0.5를 기준으로 0.5보다 낮은 값은 0으로, 0.5보다 큰 값은 1로 판단할 것이다.

하지만 세상의 모든 일이 그렇듯 우리가 예상했던 것처럼 항상 저렇게 예쁜 모양으로 나타나지는 않는다. 위의 이미지처럼 특이하지만 명확히 구분할 수 있는 모양이 나온다. 이런 경우에 대한 분류는 참고할만한 사이트들의 링크를 거는 것으로 넘어가겠다. 자세히 설명하자니 방대하고, 다른 블로그에서도 충분히 설명을 잘해주셨기 때문이다.
1. SVM (Support Vector Machine : 서포트 백터 머신)
두 범주를 잘 분류하면서 마진(margin)이 최대화된 초평면(hyperplane)을 찾는 기법으로 기본적으로 선형분류를 한다.
아래에 참고할만한 블로그 3개의 링크를 걸어놨다. 다들 참고하기를 바란다.
추가적으로 SVM과 Logistic Regression의 차이점에 대한 표를 남기겠다.
| Logistic Regression | SVM | |
| 데이터 종류 | 이미 식별된 독립 변수 | 텍스트 및 이미지와 같은 비정형 및 반정형 데이터 |
| 모델 생성 방식 | 통계적 접근 방식 기반 | 기하학적 특성 기반 |
| 과적합 | 과적합 위험 많음 | 과적합 위험 적음 |

2. Kernel SVM
상당히 복잡한 모양의 데이터들을 분류하는 방법이다. 이 또한 링크를 참고하기를 바란다.

3. Bayes Rule (베이즈 정리)
확률통계에서 사용하는 방법이다.
4. Naive Bayes (나이브 베이즈)
5. Decision Tree (의사 결정 나무) / Random Forest / 앙상블
Decision Tree Random Forest 앙상블
'인공지능 > 인공지능 이론' 카테고리의 다른 글
| 11. 차원의 저주 / PCA (0) | 2019.09.13 |
|---|---|
| 10. ROC Curve (1) | 2019.09.12 |
| 8. Regression (회귀) (0) | 2019.09.08 |
| 7. 머신러닝종류 (0) | 2019.09.08 |
| 6. Train, Valid, Test Data / CrossValidation (교차 검증) (0) | 2019.08.27 |