Curse Of Dimensionality (차원의 저주)
우리는 데이터가 많으면 많을수록 더 좋은 학습 모델을 만들 수 있다고 얘기했다. 반대로 데이터가 적을 경우, 그 데이터를 늘리기 위해 여러가지 방법들에 대해서도 이야기했다. 하지만 데이터가 적음에도 불구하고 용량이 큰 경우에 대해서는 이야기하지 않았다. 지금부터 그러한 경우에 대해서 얘기해보고자 한다. 데이터가 적은데 용량이 크다니 이게 무슨 어불성설인가! 이 말은 즉슨 데이터량은 적지만 각각의 데이터에 할당된 정보량, 즉 차원(Dimension)이 많은 경우를 뜻한다. 쉽게 이해하기 어려우니 예를 들자면 대표적으로 이미지를 들 수 있겠다. 우리가 다루는 이미지는 대부분 픽셀로 이루어져있다. 픽셀이 많을수록 고해상도이다. 하지만 이미지는 단 하나이다. 이런 경우가 차원이 많은 경우라고 볼 수 있다. 데이터(그림)는 하나이지만, 그 안에 있는 차원(픽셀)이 많은 경우 우리는 학습을 하는데 어려움을 겪게 되고 많은 데이터를 필요로 한다. 이러한 것을 Curse Of Dimensionality(차원의 저주)라고 한다.
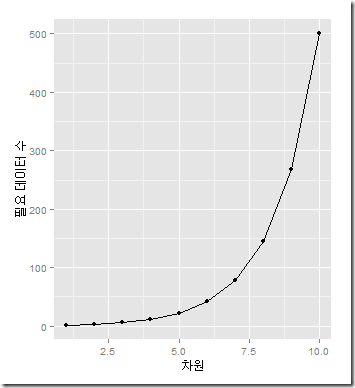
이러한 경우는 우리가 여태까지 공부해왔던 것처럼 직관이 성립하지 않으며 차원이 적으면 데이터들이 가깝게 뭉쳐있지만 차원이 크면 데이터들간의 거리가 커지면서 전체 공간에서 데이터가 차지하는 공간이 적어진다. 데이터가 차지하는 공간이 적어진다는 것은 새롭게 예측한 데이터도 훈련에 사용한 데이터와 멀리 떨어져 있을 가능성이 높다는 것을 뜻하고 예측모델을 만들기 위해 훨씬 더 많은 작업을 해야하지만 저차원보다 예측 결과가 좋지 못할 가능성이 높아진다.
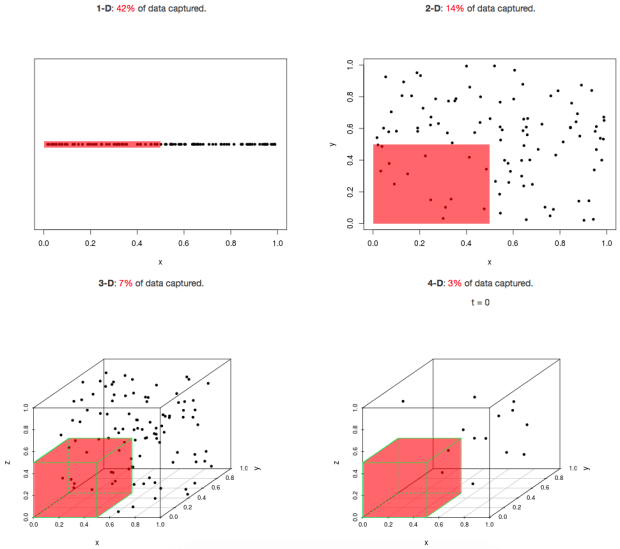
우리는 어떻게 차원의 저주에서 벗어날 수 있을까? 우선 첫째로 데이터의 양을 늘리는 방법이 있겠다. 하지만 데이터의 양을 늘리는 것도 어느정도의 한계가 존재한다. 그렇다면 어떻게 해야할까? 그 방법으로 바로 차원 축소가 있다.
Dimensionality Reduction (차원 축소)
차원 축소는 말 그대로 차원 축소이다. 어떻게 차원 축소가 차원의 저주에서 벗어날 수 있는걸까? 당연스럽게 느껴지지만 정확한 이유에 대해서는 잘 모르겠다. 이에 대한 이해를 돕기 위해 우리는 다양한 동물 중 고양이에 대해 분류하는 모델을 만드려고 한다고 가정해보자. 우리가 학습을 위해 수집한 데이터들은 다양한 픽셀(차원)의 고양이 이미지로 구성되어 있을 것이다. 또, 고양이는 먼치킨, 코숏, 아메리칸 숏헤어, 샴 등 다양한 종류의 고양이가 존재할 것이다. 이런 다양한 이미지의 전체 픽셀(차원)을 고려하여 학습하는 것은 굉장히 까다롭고 어려울 것이다. 하지만 자세히 보면 고양이를 특정 짓는 것은 일정하다. 고양이의 눈, 코, 입이 가장 대표적인 고양이의 특징일 것이다. 또한 이러한 고양이의 특징을 파악할 수 있는 픽셀(차원) 또한 한정되어있다. 이러한 경우 우리는 일정 픽셀(차원)에 대해서만 학습해도 충분히 우리가 원하는 모델을 만들어 낼 수 있다. 이러한 경우처럼 전체 차원인 관찰 공간(Observation Space)이 아닌 유의미한 특정 차원인 잠재 공간(Latent Space)에 대해서만 학습하여 원하는 모델을 만들어내기 위해 차원 축소를 사용한다.
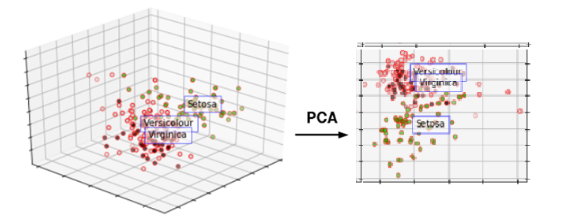
주성분 분석은 말 그대로 전체 차원에서 가장 주요한 성분을 순서대로 추출하는 기법을 말한다. 여러 변수의 값을 합쳐서 그 보다 적은 수의 주요 성분을 새로운 변수로 하여 데이터를 표현하기 때문에 차원을 축소할 때 사용할 수 있는 기법이다. PCA에 대해 친절하고 자세히 설명해주는 유튜브 영상을 첨부하겠다. 또 이 유튜브 영상에 대해 자세히 설명해주는 블로그 또한 첨부하겠다.
https://www.youtube.com/watch?v=FgakZw6K1QQ
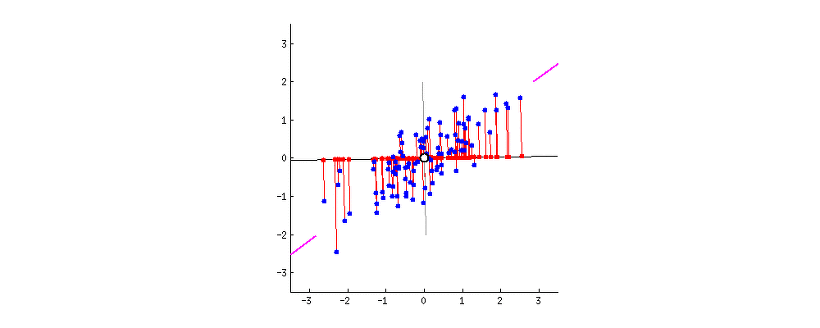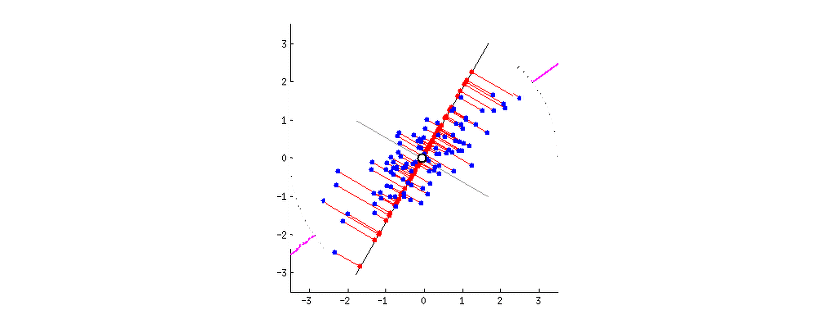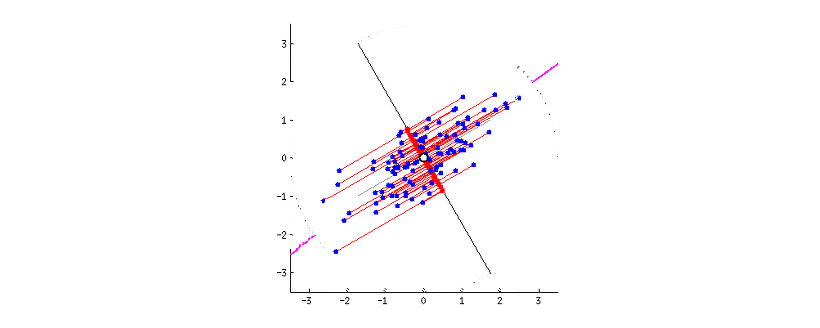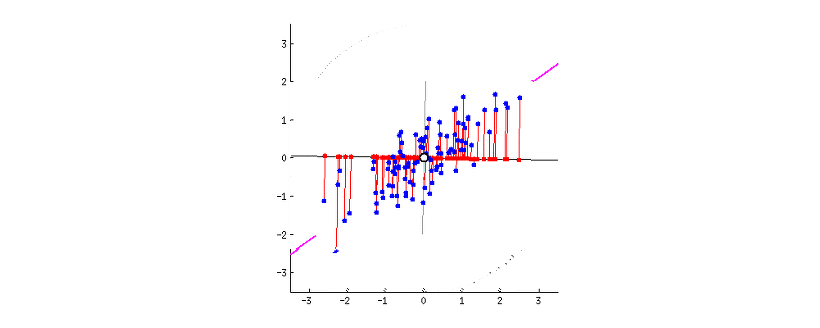
가장 폭 넓은, 즉 분산이 가장 크게 되는 축은 데이터를 가장 폭 넓게 설명할 수 있다. 따라서 분산이 가장 큰 축을 제 1주성분이라고 한다. 이처럼 분산의 정도에 따라 차등적으로 주성분을 만들어나가는데, 몇까지의 주성분을 사용하는지에 대해서는 맨 위의 PCA를 누르면 참고할 수 있는 블로그를 참고하길 바란다.
'인공지능 > 인공지능 이론' 카테고리의 다른 글
| 13. Perceptron (퍼셉트론) (0) | 2019.09.14 |
|---|---|
| 12. Clustering (0) | 2019.09.13 |
| 10. ROC Curve (1) | 2019.09.12 |
| 9. Classification (분류) (0) | 2019.09.11 |
| 8. Regression (회귀) (0) | 2019.09.08 |