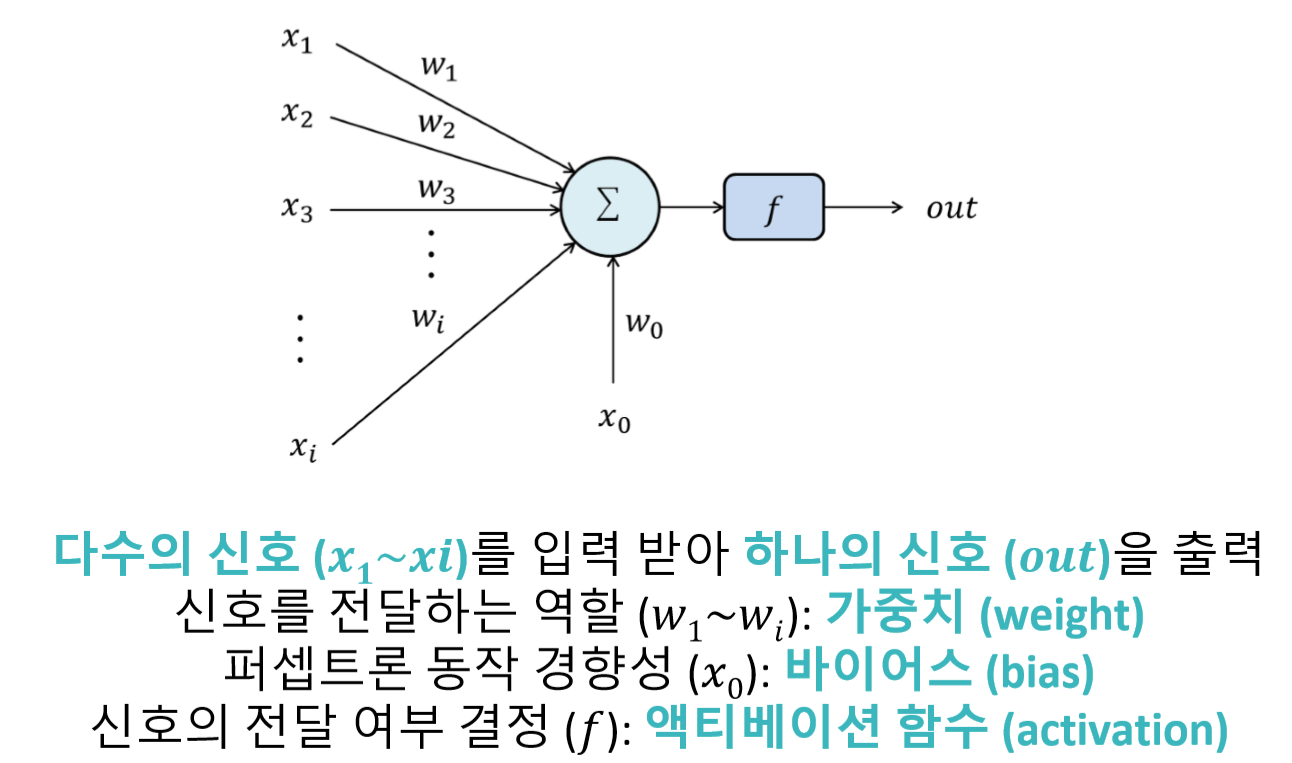
|
자료형태 |
|
|
범주형 |
명목형 |
|
순서형 |
|
|
수치형 |
이산형 |
|
연속형 |
|
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
|
# 나이브베이즈알고리즘을 이용하여 식용버섯과 독버섯 분류하기
mushroom = read.csv("c:/data/mushrooms.csv",header=T,stringsAsFactors = T)
# factor로 변환하는 이유
# factor로 변환하지 않으면 프로그램이 문자를 단지 형(string)으로만 인식하지만
# factor로 변환하면 각각의 문자를 범주로 인식하기 때문에 나이브 베이즈를 사용하는 명목형 데이터는 Factor 형태여야 함
# R은 테이블로도 데이터를 확인할 수 있음
View(mushroom)
# 결측치 확인
colSums(is.na(mushroom))
dim(mushroom) # 8124(데이터 개수) 23(컬럼 개수)
# 데이터 shuffle
set.seed(1)
train_cnt <- round( 0.75*dim(mushroom)[1] )
train_cnt # 6093
# mushroom의 1부터 8124 중 6093개(train_cnt)만큼 임의의 숫자를 뽑음
train_index <- sample( 1:dim(mushroom)[1], train_cnt, replace=F)
train_index
# 임의로 뽑힌 6093개의 인덱스들을 추출해서 train / test 로 나눔
mushroom_train <- mushroom[ train_index, ]
mushroom_test <- mushroom[-train_index, ]
nrow(mushroom_train) #6093
nrow(mushroom_test) #2031
# mushroom_train 확인
str(mushroom_train)
# 없다면 'e1071 패키지 깔기'
# install.packages('e1071')
# 나이브 베이즈 알고리즘 사용
library(e1071)
model1 <- naiveBayes(type~.,data=mushroom_train) # type~. : 예측하고자 하는 컬럼 의미
model1
result1 <- predict( model1, mushroom_test[ , -1] )
result1
library(gmodels)
CrossTable(mushroom_test[ ,1], result1)
# 어떤 laplace 값이 정확도가 가장 높을까?
temp = c()
laplace_num = c()
for (i in 1:10) {
laplace_num = append(laplace_num,i*0.001)
mushroom_test_pred = naiveBayes(type~ . , data=mushroom_train, laplace=i*0.001)
result2 <- predict(mushroom_test_pred, mushroom_test[ , -1] )
g2 <- CrossTable(mushroom_test[ ,1], result2)
g3 <- g2$prop.tbl[1]+g2$prop.tbl[4]
temp = append(temp,g3)
}
result = data.frame("laplace"=laplace_num,"정확도"=temp)
library(plotly)
plot_ly(x=~result[,"laplace"],y=~result[,"정확도"],type='scatter',mode='lines') %>%
layout(xaxis=list(title="laplace값"),yaxis=list(title="정확도"))
|
cs |

'인공지능 > 실습예제' 카테고리의 다른 글
| (R) 의사결정트리 활용하기 1 - 화장품을 구입할 고객은? (0) | 2020.06.25 |
|---|---|
| (R) 나이브베이즈알고리즘 활용하기 3 - 독감 환자입니까? (0) | 2020.06.25 |
| (R) 나이브베이즈알고리즘 활용하기 2 - 영화 장르 예측 (0) | 2020.06.25 |
| (R) KNN알고리즘 활용하기 2 - 와인 분류 (0) | 2020.06.24 |
| (R) KNN알고리즘 활용하기 1 - 유방암 분류 (0) | 2020.06.24 |