공부하려고 만든 블로그

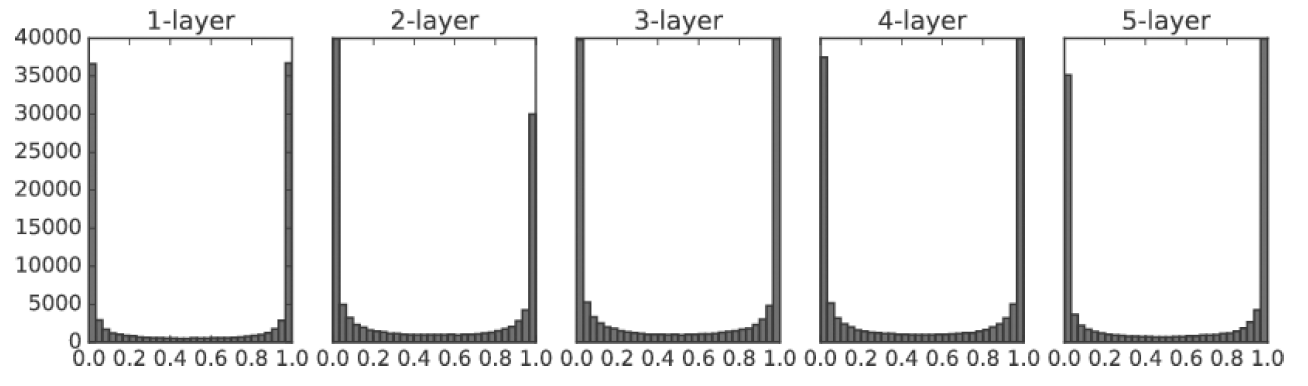
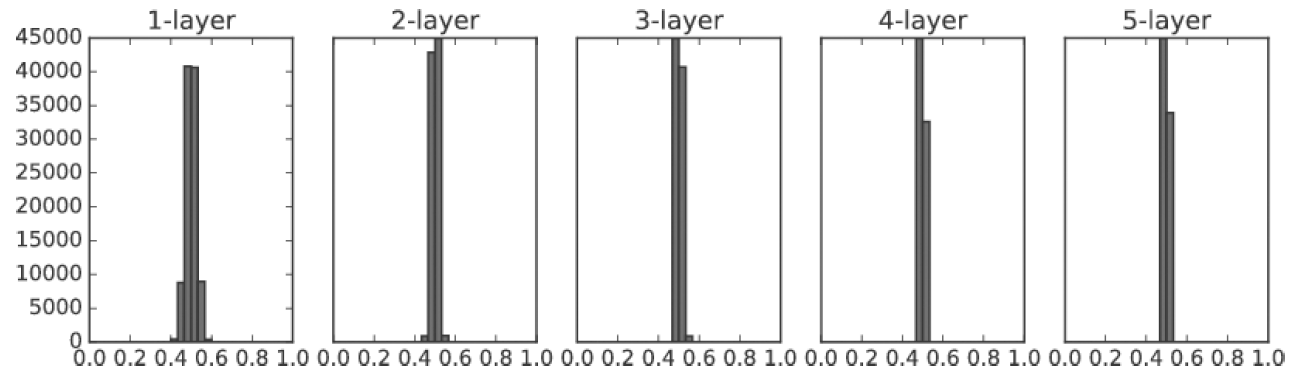
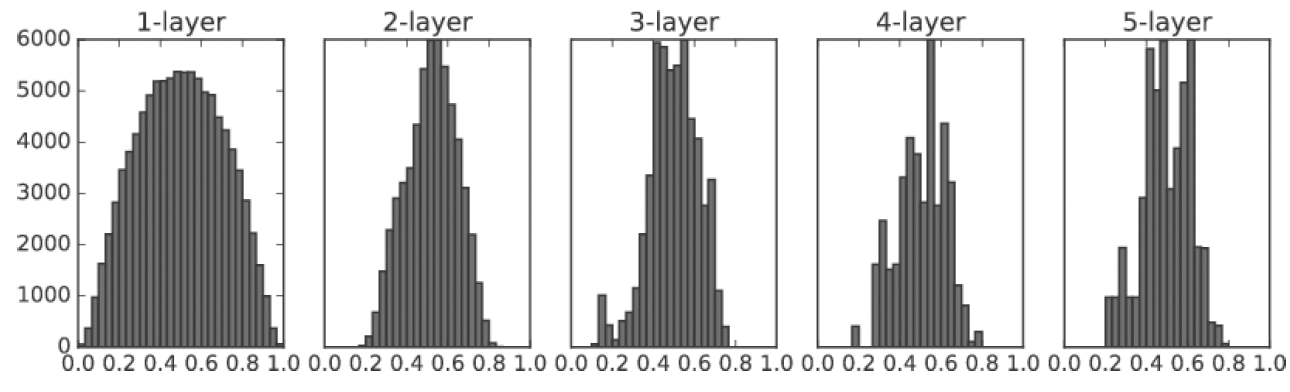
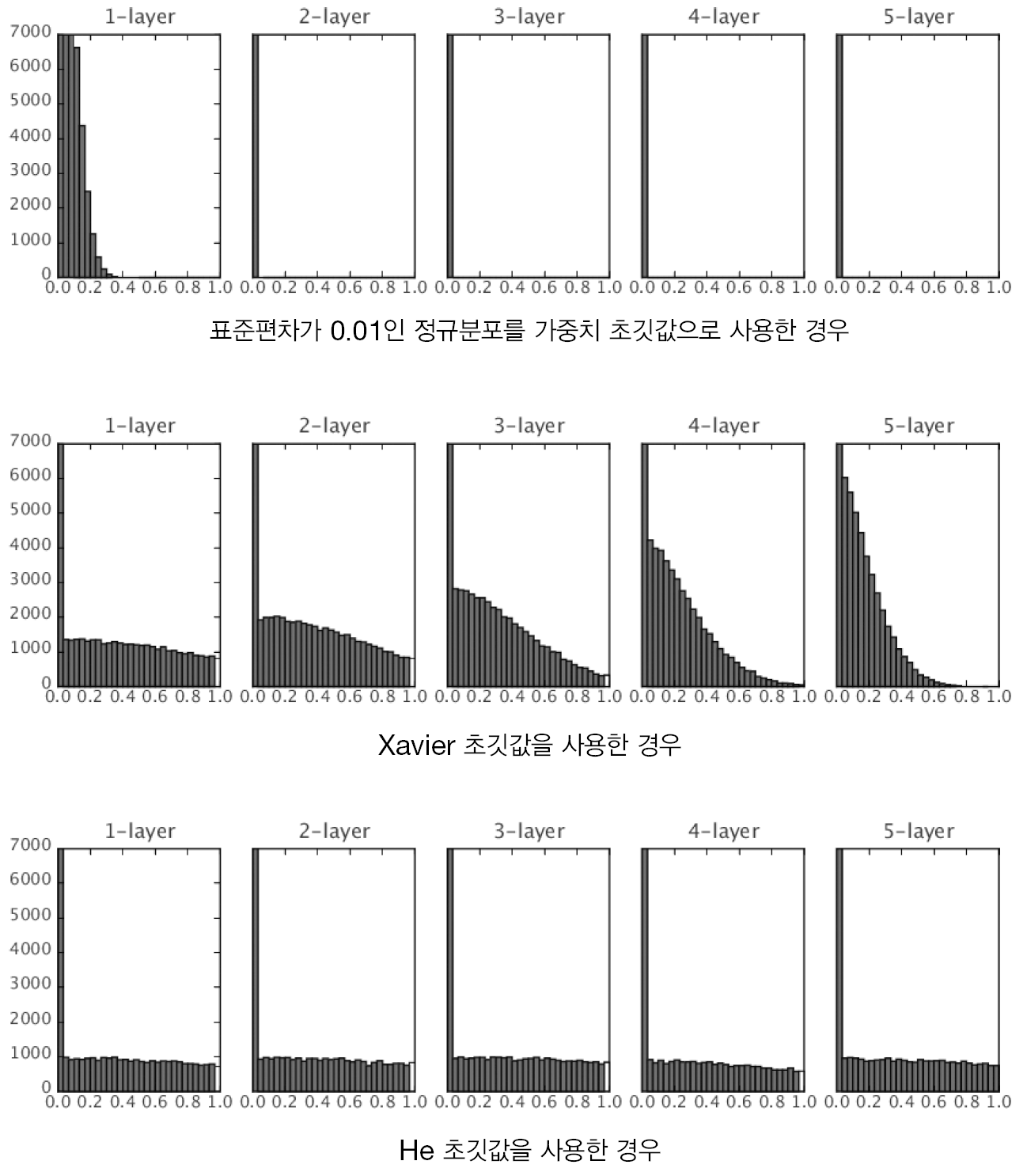
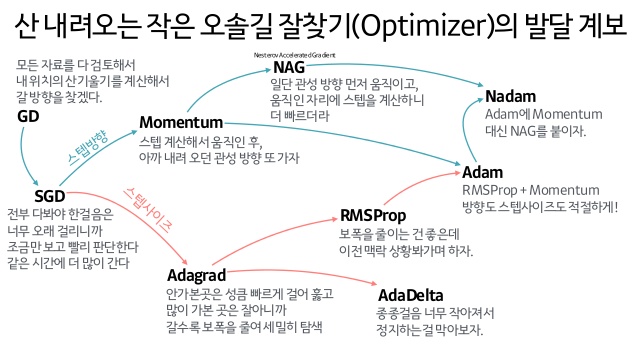
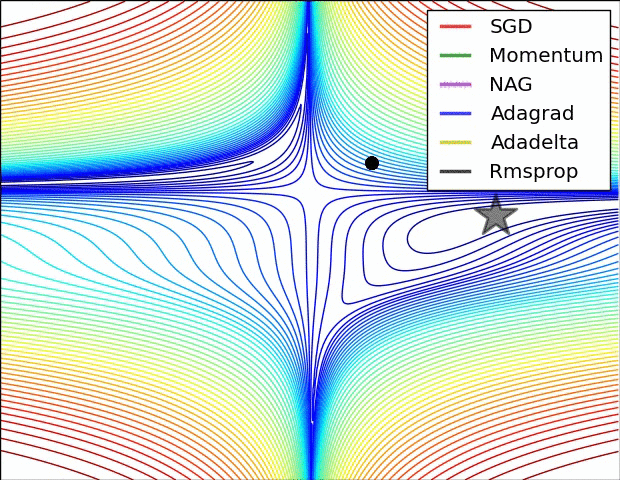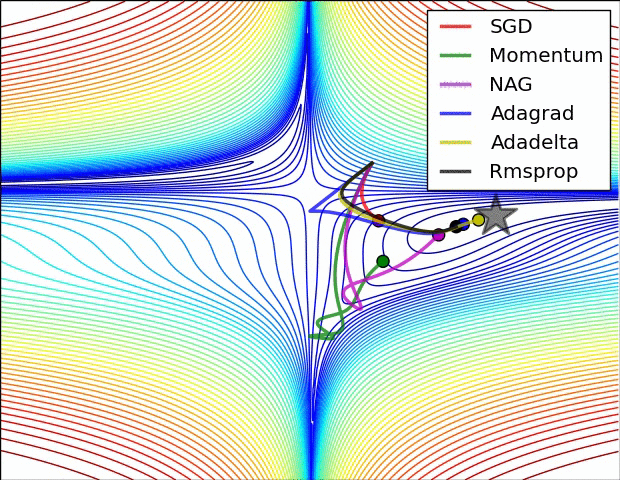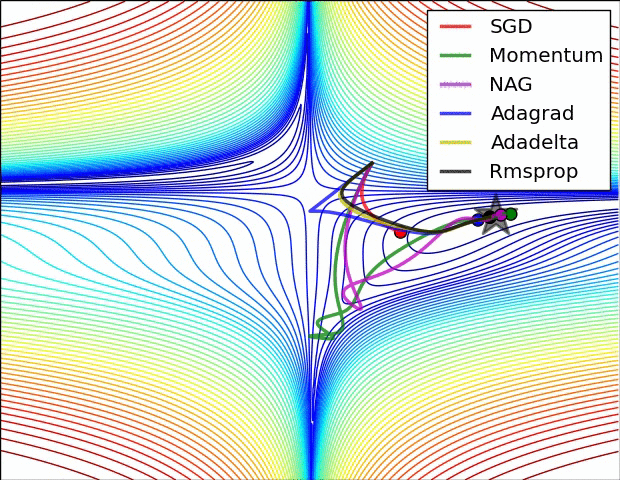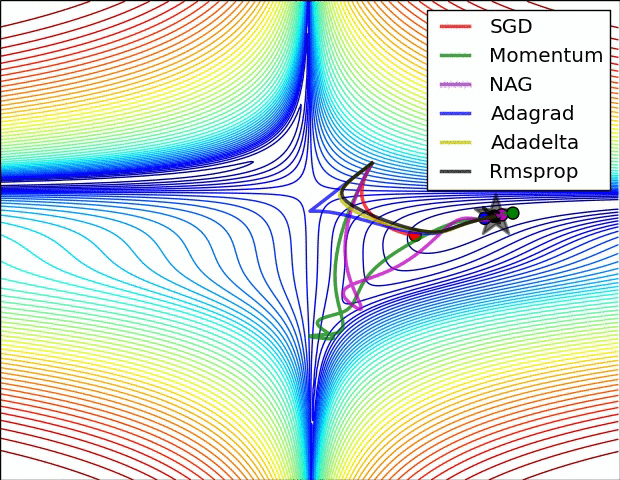
앞서 설명했던 가중치 초깃값의 중요성은 결론적으로 활성화된 값들이 고르게 분포되기 위함이었다.

그렇다면 초기에 설정하는 가중치값 말고 또 활성화 값들을 고르게 만들 수는 없을까?

배치 정규화 (Batch Normalization)

이러한 생각에서 시작된 것이 배치 정규화(Batch Normalization)이다. 배치 정규화는 활성화 함수의 출력값(활성화값)을 정규화하는 작업을 뜻한다. 배치 정규화의 장점은 다음과 같다.

• 학습을 빨리 진행할 수 있다. (학습 속도 개선)
• 가중치 초깃값에 크게 의존하지 않는다.
• 오버피팅을 억제한다.

장점이 너무 어마어마해서 다들 많이 쓰는것 같다. 앞에서 말했던 가중치 초깃값도 별로 중요치 않고, 오버피팅을 억제하기 위해 후에 기술할 드롭 아웃, 가중치 감소 등도 굳이 사용하지 않아도 되니 말이다. 이게 바로 3 in 1

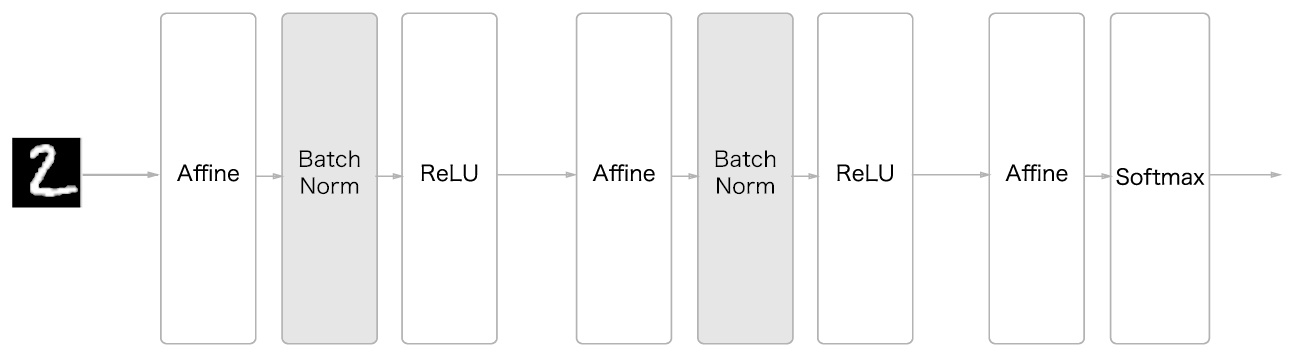
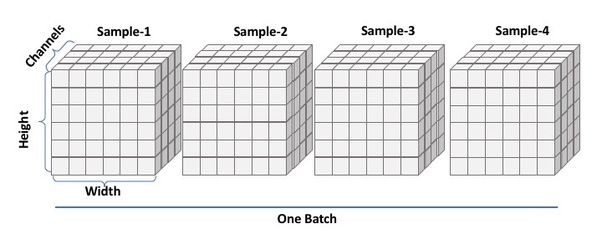
위의 이미지가 배치 정규화를 사용한 신경망이다. 여기서 Batch Norm이 배치 정규화 계층으로, 학습 시 미니배치를 단위로 정규화를 한다. 구체적으로 데이터 분포가 평균이 0, 분산이 1이 되도록 정규화한다.

이 Batch Norm이 활성화 함수의 전에 있어야 하는지, 후에 있어야 하는지에 대한 것은 논의 중이라고 하는데 자세하게 알게 되면 추가하겠다. 우선 위의 신경망은 Batch Norm의 활성화 함수 이전에 넣었다. 이렇게 Batch Norm을 신경망 구현에 사용하게 되면 데이터가 덜 치우치게 분포하게 되고, 또한 배치 정규화 계층마다 이렇게 정규화된 데이터를 확대, 이동하기도 한다.

Batch Norm도 확대와 이동의 하이퍼파라미터를 설정해야하는데, 현재 대다수의 완성된 신경망은 적절한 Batch Norm 하이퍼파라미터를 내장하고 있기 때문에 크게 신경쓰지 않아도 된다. 하지만 직접 만들겠다면 다른 얘기

과적합, 오버피팅 (Overfitting)

오버피팅이란 신경망이 훈련 데이터에만 지나치게 적응되어 그 외의 데이터에는 제대로 대응하지 못하는 상태를 말한다. 오버피팅은 매객변수가 많고 표현력이 높은 모델일수록, 훈련 데이터가 적을수록 많이 일어난다.

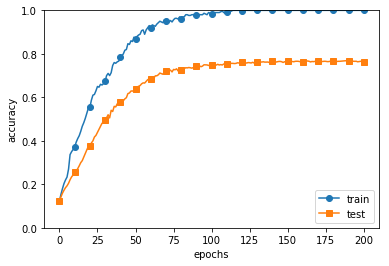
가중치 감소 (Weight Decay)

오버피팅을 억제하는 방법으로 가중치 감소가 있다. 이는 학습 과정에서, 큰 가중치에 대해서는 그에 상응하는 큰 페널티를 부과하여 오버피팅을 억제하는 방법이다. 오버피팅은 가중치 매개변수의 값이 커서 발생하는 경우가 크기 때문에 가중치 감소는 예로부터 오래 써온 오버피팅 억제 방법이며 모든 가중치 각각의 손실함수에 L2노름(각 원소의 제곱들을 더해서 루트를 씌운 값)을 더하여 구한다.

드롭아웃 (Dropout)

가중치 감소는 간단하게 구현할 수 있고 어느정도 과적합을 방지할 수 있지만 신경망이 깊어지고 복잡해질수록 과적합을 막기 어려워진다. 이러한 경우, 드롭아웃을 사용한다.

드롭아웃이란 뉴런을 임의로 삭제하면서 학습하는 방법으로 훈련 시 은닉층의 뉴런을 무작위로 골라 삭제한다. 삭제된 뉴런은 신호를 전달하지 않기 때문에 학습에 사용되지 않는다. 이렇게 학습을 반복할 때마다 무작위로 뉴런을 삭제하며 학습을 하다가 실제 시험 데이터에서는 모든 뉴런에 신호를 전달한다. 시험 때는 각 뉴런의 출력에 훈련 때 삭제 안 한 비율을 곱하여 출력한다.

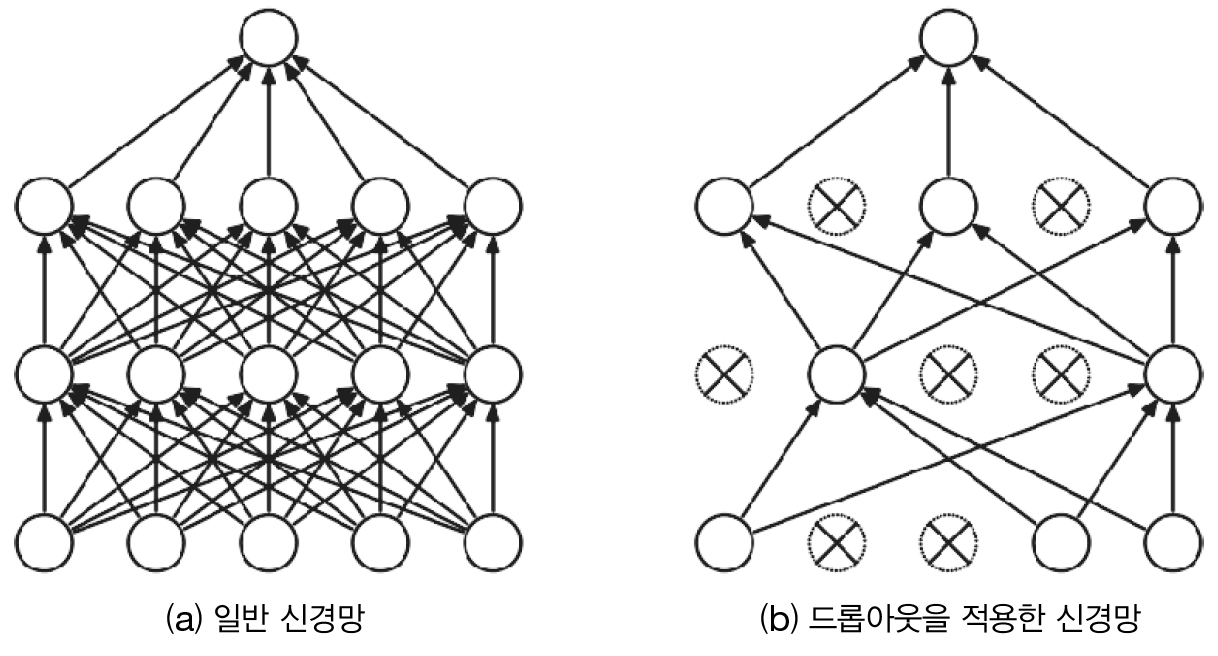
드롭아웃은 기계학습의 앙상블 학습(Ensemble Learning)과 비슷하다. 앙상블 학습이란 개별적으로 학습시킨 여러 모델의 출력을 평균 내 추론하는 방식이다. 드롭아웃 또한 학습 때 뉴런을 무작위로 삭제하는 행위가 매번 다른 모델을 학습시키는 것과 같은 맥락으로 이해할 수 있다. 또한 추론 시, 뉴런의 출력에 삭제한 비율을 곱함으로써 앙상블 학습에서 여러 모델의 평균을 내는 것과 같은 효과를 얻을 수 있다. 따라서 드롭아웃은 앙상블과 같은 효과를 신경망에 적용했다고 볼 수 있다.

초기 가중치 값의 중요성

가중치 초기값은 신경망 학습에 있어서 매우매우 중요하다. 잘 설정한 초기 가중치가 신경망 전체의 성능을 좌우한다고해도 과언이 아니기 때문이다.

가중치 초기값은 균일한 값으로 설정되면 안된다. 왜냐하면 오차역전파법에서 모든 가중치의 값이 똑같이 갱신되기 때문이다. 이렇게 되면 가중치를 여러개 갖는 의미가 없다. 따라서 가중치가 고른(대칭적인 구조) 상황을 막기 위해 가중치 초깃값은 균일하지 않은, 무작위의 값으로 설정되야 한다.

그렇다면 가중치 초기값은 단순히 무작위로만 만들어지면 되는걸까?

이에 대한 내용으로는 은닉층에서 사용하는 활성화함수(Sigmoid, ReLU)를 살펴봐야 한다.

Xavier 초깃값 (Sigmoid에서 사용)

가중치의 초깃값은 은닉층 활성화값들에 영향을 미친다.

표준편차가 1인 정규분포로 초기 가중치 분포를 지정한 경우, 각 층의 활성화값들이 0과 1에 치우쳐져 있다. Sigmoid 함수는 값이 0 또는 1에 치우쳐지면 기울기가 0이 되기 때문에, 역전파의 기울기 값이 점점 작아지다 사라진다. (미분이 0이니까) 이러한 문제점을 기울기 소실(Gradient Vanishing)이라고 한다. 따라서 이 초기 가중치값은 층이 깊어지면질수록 제대로 학습을 하지 못한다.

표준편차가 1인 경우와 달리 0 또는 1로 치우치진 않아 기울기 소실 문제가 일어나지는 않았지만 활성화값들이 0.5로 치우쳐진 것 또한 문제이다. 이는 다수의 뉴런의 거의 같은 값을 출력한다는 뜻으로 여러 뉴런을 갖는 이유가 없어지기 때문이다. 이러한 문제점을 표현력을 제한한다는 관점에서의 문제점이라고 한다.

결국 초기 가중치값은 활성화값들이 0 또는 1로 치우쳐지지 않게 하면서도 표현력을 제한하지 않도록 고르게 분포되도록 해야한다.

Sigmoid에 대해서 활성화값들을 고르게 분포되게 해주는 초기 가중치값은 Xavier 초깃값으로, Xavier 초깃값은 일반적인 딥러닝 프레임워크들이 표준적으로 사용하고 있다. Xavier 초깃값은 앞 계층의 노드가 n개일 때 표준편차가 1/sqrt(n)인 분포를 사용한다. Xavier 초깃값을 사용하면 앞 층에 노드가 많을수록 대상 노드의 초깃값으로 설정하는 가중치가 좁게 퍼진다. 쉽게 생각해 데이터가 적당히 퍼져있다는 말이다. 따라서 Xavier 초깃값은 Sigmoid 함수가 표현력의 제한도 받지 않으면서 효율적으로 학습할 수 있도록 한다.

추가적으로 위의 이미지를 보면 층이 깊어질수록 약간씩 일그러지는 형태를 볼 수 있는데, 이러한 일그러짐은 Sigmoid함수 대신 tanh 함수를 사용하면 개선된다.

He 초깃값 (ReLU에서 사용)

Xavier 초깃값은 활성화 함수가 선형일 때 사용한다. Sigmoid 함수와 tanh 함수는 좌우가 대칭이기 때문에 중앙이 선형적이라고 볼 수 있기 때문에 Xavier 초깃값을 사용한다. 하지만 ReLU는 대칭적이지 않기 때문에 ReLU에 맞춰 초깃값을 설정해야한다. 이 초깃값이 He 초깃값이다. 사실 He 초깃값은 Xavier 초깃값과 크게 다르지는 않다. He 초깃값은 앞 계층의 노드가 n개일 때 표준편차가 sqrt(2/n)인 정규분포를 사용하기 때문이다. 이러한 이유는 ReLU는 음의 영역이 0이기 때문에 더 넓게 분포시켜야 했기 때문이라고 직관적으로 해석할 수 있다.

위의 그림을 보면 ReLU도 표준편차가 0.01인 경우 0으로 치우쳐진다. 또한 Xavier 초깃값을 사용하면 초반에는 고르게 분포되다가 층이 깊어질수록 치우치기 시작한다. 이는 층이 더 깊어지면 표준편차가 0.01인 경우와 같이 기울기 소실 문제가 발생한다. He 초깃값을 보면 층이 깊어져도 균일하게 분포되어있기 때문에 학습이 잘 될 것으로 (역전파가 잘 될 것으로) 예상할 수 있다.

결론적으로 현재까지는 Sigmoid나 tanh 등의 S자 모양 곡선 활성화 함수를 사용할 경우 Xavier 초깃값을 사용하고, ReLU를 사용할 때는 He 초깃값을 사용하는 것이 가장 좋은 초기 가중치값이라고 볼 수 있다.

다양한 최적화 알고리즘

최적화란 매개변수의 최적값을 찾는 것을 의미한다. 지금껏 설명해온 최적화 기법은 SGD, 확률적 경사 하강법 뿐이었다. 하지만 SGD에는 단점이 있다. 필자는 이 단점을 해결해나가는 다양한 최적화 알고리즘에 대해 설명하고자 한다.

위의 이미지는 블로그에서 갖고왔다. 이미지가 너무 완벽하게 설명되어 있어서 사실 뭘 더 설명하기가 애매할 지경이다. 따라서 수식과 함께 최적화 알고리즘별 특징을 짚고 넘어가겠다. 아래 내용을 이해 못하겠으면 그냥 위의 이미지만 이해해도 됨 갓벽

경사하강법

경사하강법은 무작정 기울어진 방향으로 진행하기 때문에 상당히 무식하다 비효율적이다. 또한 그림에서처럼 지그재그로 탐색하는 근본 원인이 기울어진 방향이 본래의 최솟값과 다른 방향을 가리켜서라는 점 또한 SGD의 단점이다.

모멘텀 (Momentum)

모멘텀은 운동량을 뜻하는 단어로, 더 효율적인 탐색을 위해 물리 법칙을 구현한 것이다.

v는 속도를 의미하며, 기울기 방향으로 힘을 받아 물체가 가속된다는 물리 법칙을 의미한다. 모멘텀 알고리즘을 최적화에 사용할 경우 가중치 매개변수는 공이 그릇 바닥을 구르는 듯한 움직임을 보인다.

SGD와 비교하면 지그재그 정도가 덜하다.

AdaGrad

신경망 학습에서 η, 학습률은 매우 중요하다. 따라서 이 학습률을 효과적으로 정하는 것이 매우 중요하다. 학습률을 효과적으로 정하는 기술 중 하나로 학습률 감소라는 것이 있는데, 이는 학습을 진행하면서 학습률을 점차 줄여나가는 방법으로 처음에는 크게 학습하다가 점점 조금씩만 학습하게 되는 기술이다.

AdaGrad는 이러한 학습률 감소를 각각의 매개변수에 맞춰 적응적으로 학습률을 조정하며 학습을 진행한다.

위의 식을 보면 알다시피, AdaGrad는 매개변수를 갱신할 때 1/sqrt(h)를 곱해 학습률을 조정한다. 이는 매개변수의 원소 중에서 크게 갱신된 (많이 움직인) 원소는 학습률이 낮아진다는 뜻으로, 각각의 매개변수마다 학습률 감소가 다 다르다.

y축 방향을 보면 기울기가 커 초반에는 크게 움직이지만, 움직임에 비례해 갱신 정도도 큰 폭으로 줄어들면서 효율적으로 최솟값을 향하는 것을 볼 수 있다.

RMSProp

AdaGrad는 과거의 기울기를 제곱하여 계속 더해가기 때문에 학습을 진행할수록 갱신 강도가 약해진다. 따라서 학습을 많이 반복하면 어느 순간 갱신량이 0이 되는 순간이 온다. 이러한 문제점을 개선하는 것이 RMSProp이다.

RMSProp는 과거의 기울기를 계속해서 누적하는 것이 아니라 먼 과거의 기울기는 서서히 잊고 새로운 기울기의 정보를 크게 반영한다. 이를 지수이동평균(EMA)이라 하며 과거 기울기의 반영 규모를 기하급수적으로 감소시킨다.

Adam

Adam은 모멘텀과 AdaGrad를 합친 것으로, 더 효율적으로 빨리 탐색할 수 있으며 하이퍼파라미터의 편향 보정 또한 진행된다는 특징이 있다.

어떤 갱신 방법이 좋느냐, 라고 묻는다면 모른다. 가 대답이다. 안타깝기 짝이 없는 인공지능 세계는 영화와 달라 수많은 알고리즘들 중 다양한 조합을 시도하며 알고리즘을 구성하는 수개의 하이퍼 파라미터들을 대입하여 최적의 결과를 찾는, 결론적으로는 완벽한 노가다의 세계이기 때문이다. 갓 블래스 유,,,

앞서 설명했던 SGD와 같은 것을 우리는 수치 미분이라고 한다. 수치 미분을 사용하는 이유는 오차를 줄여나가 신경망의 최적의 매개변수(가중치,편향)를 찾아가기 위해서이며, 더 자세하게 설명하자면 가중치의 매개변수에 대한 손실 함수의 기울기를 구하기 위해서이다.

수치 미분은 구현은 단순하지만 계산이 오래걸린다는 단점이 있다. 신경망은 수만개의 데이터를 수십개의 은닉층으로 학습시키기 때문에 계산이 빨라야 한다. 따라서 우리는 가중치 매개변수의 기울기를 효율적으로 계산하는 방법이 필요하다.

계산 그래프

딥러닝 학습서의 바이블 <밑바닥부터 시작하는 딥러닝>의 '오차역전파법'의 내용을 완벽하게 알려주는 블로그의 링크를 기재했으니 참고하길 바란다. 책이 너무 완벽해서 구입을 추천하지만 오차역전파법 자체만을 공부하고 싶다면 블로그에 기재된 내용만으로도 충분하며, 보충 설명이 필요할 경우 유튜브를 참고하길 바란다.

저자는 오차역전파법에 대해 설명할 때 수식보다는 계산 그래프를 활용한다. 그 이유는 우선 계산 그래프가 수식에 비해 상당히 직관적으로 받아들여지고 국소적 계산을 볼 수 있기 때문이다. 국소적 계산이란 뭘까?

국소적 계산

국소적 계산은 계산 전체에서 어떤 일이 벌어지든 상관없이 자신과 관련된 정보만으로 결과를 출력한다. 즉, 매우 복잡한 수식도 까보면 수많은 연산들의 합과 곱이며, 이 수많은 연산들을 하나씩만 놓고 보면 사실 별거없다. 라는게 국소적 계산의 뜻이다. 또한 국소적 계산은 연산 하나하나들의 결과를 보관할 수 있다. 따라서 우리는 전체로 향하는 과정을 간결하면서도 전부 볼 수 있게 된다. 이러한 국소적 계산의 효과 덕에 우리는 효율적으로 역전파를 구할 수 있다. 여기서 역전파란, 위의 계산 그래프를 볼 때 진행 방향(왼쪽에서 오른쪽)의 반대 방향(오른쪽에서 왼쪽)을 의미하며 순전파(→)의 역방향(←)으로 미분 값을 전달한다.

가령 우리가 사과값이 오를 때, 최종 금액이 얼마나 변화하는지를 알고 싶을 때 우리는 미분을 사용한다. 미분의 정의는 순간적인 변화량이기 때문이다. 따라서 역전파는 국소적 미분을 전달하며 각 변수의 미분을 효율적으로 구할 수 있게 도와준다.

연쇄법칙

위의 수식은 합성 함수를 보이기 위한 수식이다.

합성 함수란, 여러 함수로 구성된 함수이며 연쇄법칙은 합성 함수의 미분에 대한 성질이다.

연쇄 법칙이란 합성 함수의 미분은 합성 함수를 구성하는 각 함수의 미분의 곱으로 나타낼 수 있다는 것이다.

이과생이라면 위의 수식이 익숙할 것이다. 기억에는 고등학교때 수학도 가끔은 이렇게 풀었던 것 같다. 어쨌든, 위의 수식을 풀어 말하자면 여러개의 변수로 이루어진 함수에서 몇몇 변수를 하나의 변수로 새롭게 생성해 각각을 미분하여 곱하는게 원래의 함수를 미분하는 것과 같다는 말이다. 이 연쇄 법칙이 계산 그래프를 활용하여 역전파를 이해하는 중요한 키워드가 될 것이기 때문에 최소한 위의 수식에 대해서는 확실히 이해하고 넘어가길 바란다. 복잡해 보이는 것에 비해 의외로 별 내용이 없다.

일반 연산(덧셈, 곳셈) 노드의 역전파

덧셈 노드의 역전파는 입력 값을 그대로 흘려보낸다.

곱셈 노드의 역전파는 순전파 때의 입력신호들을 서로 바꿔 곱해 흘려보낸다.

더보기

 

활성화 함수 역전파

ReLU 계층

ReLU의 역전파는 순전파의 입력인 x가 0보다 크면 상류값을 그대로 하류로 흘려보내고 x가 0보다 작으면 0을 보낸다.

Sigmoid 계층

Sigmoid같은 경우는 설명이 복잡하므로 유튜브를 참고하길 바란다.

결론적으로 Sigmoid의 역전파는 순전파의 출력 y만으로 계산할 수 있다.

Affine 계층

Affine Transformation, 어파인 변환은 행렬의 곱을 의미한다. 신경망은 입력층에서 은닉층으로 데이터를 옮길 때 데이터와 가중치, 편향에 대해 행렬곱을 진행하였는데 이러한 처리를 Affine 계층이라고 한다. Affine 계층은 결론적으로 행렬의 곱을 진행하기 위해서 행렬의 차원을 일치시키는게 핵심이다.

Affine 계층이 이제껏 설명했던 역전파들과 다른 점은 '스칼라 값'이 아닌 '행렬 값'이라는 것이다. 따라서 Affine 계층의 역전파는 전치행렬과 미분된 행렬의 행렬곱이다. 여기서 왜 전치행렬을 곱하는지에 대한 이유는 자코비안 미분을 알아야한다. 어쨌든 역전파된 행렬곱을 하기 위해서는 전치행렬과 미분된 행렬의 위치를 잘 배치해야 한다.

배치(Batch)용 Affine 계층

이번에는 데이터를 N개 묶어 순전파하는 배치용 Affine 계층에 대해 생각해보자.

Batch는 데이터가 기존에 1x2 의 형상을 한 행렬이었다면 Nx2의 형상을 한 행렬로 변환됐을 뿐, 기존의 Affine 계층과 방식은 똑같다.

출력층 활성화 함수의 역전파

Softmax

Softmax 계층 또한 수식 자체는 아주 많이 매우 복잡하다. 이에 대한 자세한 부분은 여기를 참고하길 바란다. 여기서는 결론만 말할건데 결국 Softmax의 역전파는 신경망의 출력값과 정답 레이블의 오차를 앞 계층에 전달한다는 것이다. 신경망 학습의 목적은 신경망의 출력(Softmax의 출력)이 정답 레이블과 가까워지도록 가중치 매개변수의 값을 조정하는 것(최적화 : Optimization)이다. 따라서 신경망의 출력과 정답 레이블의 오차를 효율적으로 앞 계층에 전달해야 한다.

예를 들어보겠다. 정답 레이블이 [0 1 0]이고 Softmax 계층이 [0.3 0.2 0.5]를 출력했다고 하자. 이 Softmax의 출력값은 3번째 인덱스를 가장 높은 확률로 잡고 정답 레이블의 인덱스는 0.2로 예측하기 때문에 매우 나쁜 학습률을 보이고 있다. 이 때 Softmax의 역전파는 [0.3 -0.8 0.5]를 앞 계층에 전달한다. 그 결과 앞 계층들은 큰 오차를 통해 크게 재학습된다.

만약 정답 레이블이 [0 1 0]이고 Softmax 계층이 [0.01 0.99 0]일 경우 오차는 [0.01 -0.01 0]이다. 따라서 이런 경우는 오차가 매우 적으므로(학습을 잘 했으므로) 역전파를 통해 새롭게 학습하는 정도도 작아진다.

여기서 Softmax 함수(분류)의 손실 함수로 교차 엔트로피 오차를 사용하는 이유와, 항등 함수(회귀)의 손실 함수로 오차제곱합을 사용하는 이유가 나타난다. 각각의 함수에 손실 함수를 맞춰준 이유는 이 손실 함수들을 쓰면 각각의 함수들의 역전파 값이 예측값 - 정답 레이블로 말끔하게 떨어지기 때문이다.

지금까지 설명한 오차역전파법은 가중치 매개변수의 기울기를 구하는데 이용된다. 수치 미분으로 가중치 매개변수의 기울기를 구현할 수 있지만 수치 미분의 계산이 오래 걸리기 때문에 그보다 효율적인 오차역전파법을 사용했다. 만약 본인이 직접 오차역전파를 구현한다면 수치 미분의 결과와 오차역전파의 결과를 비교하여 검증하면 된다. 컴퓨터의 계산이 아주 정밀하진 않아서 두 값이 완벽하게 일치하긴 어렵지만 오차가 거의 0에 가까우면 잘 구현한 것이고, 차이가 너무 크다면 잘못 구현한 것이니 눈물을 머금고 잘 만들길 바란다.

앞서 신경망을 구성하기 위해서 활성화 함수, 가중치 등이 필요하다는 것을 설명했다. 위의 그림은 인공 신경망이다. 왼쪽의 그림은 은닉층이 1개이고 오른쪽 그림은 은닉층이 3개이다. 위의 선만 봐도 알 수 있다시피 신경망은 깊이가 깊어질수록, 은닉층의 노드 수가 많으면 많을수록 계산이 복잡해진다. 하지만 우리는 데이터 한 두개를 학습시키는 것이 아니라 수천, 수만개의 데이터를 학습시킨다. 우리는 인간이 할 수 있는 일이지만 더 정확하면서도 빠르게 예측, 분류하기 위해 인공지능을 사용하고자 한다. 어떻게 해야 수많은 은닉층을 가진 신경망도 빠르게 데이터를 학습시킬 수 있을까?

배치(Batch)

우리는 인공신경망에 10만개의 데이터를 학습시키고자 한다. 이 10만개의 데이터를 어떻게 해야 빠르게 학습시킬 수 있을까? 컴퓨터의 핵심인 CPU는 결국에는 계산이 주요한 능력이기 때문에 계산이 매우 빠르다. 따라서 우리는 데이터를 1개씩 입력받아 총 10만번의 연산을 진행하는 것보다 한번에 큰 묶음으로 데이터로 입력받아(Batch) n번의 연산을 진행하는 것이 더 빠르다. 즉, 느린 I/O를 통해 데이터를 읽는 횟수를 줄이고 CPU나 GPU로 순수 계산을 하는 비율을 높여 속도를 빠르게 할 수 있다는 뜻이다. 또한 수치 계산 라이브러리 대부분이 큰 배열을 효율적으로 처리할 수 있도록 고도로 최적화되어 있기 때문에 Batch(묶음)로 데이터를 입력받아 학습시키는 것이 속도 측면에서 효율적이다.

그렇다면 미니배치 학습이라는 것은 무엇일까?

미니배치 (Mini-Batch)

미니배치를 설명하기에 앞서 데이터를 하나씩 학습시키는 방법과 전체를 학습시키는 방법의 장단점에 대해 소개하겠다.

데이터를 하나 하나씩 신경망에 넣어 학습을 시키면 우선 장점으로는 신경망을 한번 학습시키는데 소요되는 시간이 매우 짧다는 것이다. 하지만 데이터를 하나씩 입력받으면 계산 속도가 사실상 늦어진다. 우리는 대부분 딥러닝에 GPU를 많이 사용하는데 그 이유가 GPU의 병렬처리에 있다. 하지만 데이터를 한개씩 넣어 인공지능을 학습시키면 사실상 GPU의 병렬처리를 사용하지 않으니 그만큼 자원 낭비가 된다. 또한 오차를 줄이기 위해 사용하는 Loss Function에서 최적의 파라미터를 설정하는데 상당히 많이 헤매게 된다.

전체 데이터를 입력하는 경우는 한번에 여러개의 데이터에 대해서 신경망을 학습시킬 수 있으므로 오차를 줄일 수 있는 cost function의 최적의 parameter를 하나씩 학습하는것보다 빠르게 알아낼 수 있다. 하지만 전체 데이터를 학습시키기 때문에 신경망을 한 번 학습시키는데 소요되는 시간이 매우 길다.

위의 문제점과 장점을 적절히 섞은 것이 바로 미니 배치이다. 미니 배치는 SGD(Stochastic Gradient Descent : 확률적 경사 하강법)와 배치를 섞은 것으로 전체 데이터를 N등분하여 각각의 학습 데이터를 배치 방식으로 학습시킨다. 따라서 최대한 신경망을 한 번 학습시키는데(iteration) 걸리는 시간을 줄이면서 전체 데이터를 반영할 수 있게되며 효율적으로 CPU와 GPU를 활용할 수 있게 된다.

에폭 (Epoch)

Epoch는 인공 신경망에서 전체 데이터 셋에 대해 한 번 학습을 완료한 상태를 의미한다. 신경망은 최적의 가중치와 기타 파라미터를 찾기 위해서 역전파 알고리즘(backpropagation algorithm)을 사용한다. 역전파에는 파라미터를 사용하여 입력부터 출력까지의 각 계층의 weight을 계산하는 과정인 순방향과 반대로 거슬러 올라가며 다시 한 번 계산 과정을 거쳐 기존의 weight을 수정하는 역방향으로 나뉜다. 이 순방향과 역방향을 모두 완료하면 한 번의 Epoch가 완료됨을 의미한다. 더 쉽게 말하자면 1에폭은 학습에서 훈련 데이터를 모두 소진했을 때의 횟수에 해당한다.

위의 그림에서 손실함수라는 것은 Loss Function, 즉 Cost Function을 의미한다.

예를 들어 훈련 데이터 10000개를 100개의 미니배치로 학습할 경우, 최적의 가중치를 구하기 위해 SGD를 100번 반복해야 모든 훈련 데이터를 학습에 활용하기 때문에 100회가 1에폭이 된다.

위의 그림의 손실함수(Loss Function)에 대해 더 자세히 설명하자면 손실함수란 Loss Function, 혹은 Cost Function이라고도 하며, 신경망에서 내놓는 결과값과 실제 결과값 사이의 차이를 정의하는 함수이다. 우리는 이 손실함수의 값이 최소값이어야 가장 좋은 신경망을 만들었다고 할 수 있다. 가장 많이 쓰는 손실 함수로 오차 제곱합(Sum of Sqaures for Error)와 교차 엔트로피 오차(Cross Entropy Error)가 있으며, 오차 제곱 합은 회귀에 주로 사용하고, 교차 엔트로피 오차는 분류에 주로 사용한다.

그리고 필자는 처음에 미니배치를 공부할 때 수만건의 데이터 중에서 n개만큼의 데이터를 임의로 추출하기 때문에 당연히 복원 추출이라고 생각했는데 (왜냐하면 데이터 개수가 매우 많으면서 데이터 전체를 표현해야하기 때문에), Epoch의 개념에서는 전체 데이터셋을 사용해야 1Epoch가 된다는 것을 읽으며 골머리를 앓았다.

배치, 혹은 미니배치학습을 할 때 배치는 복원 추출인가? 비복원 추출인가?

이에 대한 해답을 정확히 알 수는 없었으나, 어쨌든 복원 추출이나 비복원 추출이나 사실상 크게 다르지 않다는게 결론이다. 이에 대한 이유는 데이터가 매우 많기 때문이다. 수많은 데이터 중에서 임의의 개수로 임의의 데이터를 추출하는 것을 n번 반복하면 사실상 비복원 추출이나 복원 추출이나 전체 데이터셋을 사용한다고 볼 수 있기 때문이다.

확률적 경사 하강법 (SGD : Stochastic Gradient Descent)

SGD는 신경망을 학습할 때마다 가중치를 갱신한다. 기존의 경사 하강법과 개념이 다르지 않은데, 확률적이라는 말이 앞에 붙은 이유는 학습할 때마다 가중치를 갱신하기 때문에 학습할 때마다 신경망의 성능이 들쑥날쑥 변하면서 정답에 가까워지기 때문에 '무작위적'으로 보이기 때문이다. 

SGD이외에도 배치에 대한 자세한 설명과 BGD에 대해 알고 싶다면 블로그를 참고하길 바란다.