import numpy as np
N = int(input('크기를 입력하세요:'))
a = np.random.randint(1000, size=N)
# 버블정렬을 할 때 loop 횟수가 비교적 적은 것
def bubble_sort(data) :
# loop = 0
while 1 :
count = 0
for i in range(len(data)-1) :
if data[i] > data[i+1] :
temp = 0
temp = data[i]
data[i] = data[i+1]
data[i+1] = temp
else :
count += 1
# loop+=1
if count == len(data)-1 :
break
return data # , loop
print(bubble_sort(a))
##########################################################
# 위와 비교했을 때 비교적 loop 횟수가 많은 것
def bubble_sort_ez(data) :
# loop = 0
for j in range(len(data)) :
for i in range(len(data)-1) :
if data[i] > data[i+1] :
temp = 0
temp = data[i]
data[i] = data[i+1]
data[i+1] = temp
# loop += 1
return data # , loop
print(bubble_sort_ez(a))
###########################################################
# 재귀함수로 풀이
a = [1,4,3,2,5,8,7,10]
def bubble_sort(data) :
count = 0
for i in range(len(data)-1) :
if data[i] > data[i+1] :
temp = data[i]
data[i] = data[i+1]
data[i+1] = temp
count += 1
if count == 0 :
return data
return bubble_sort(data)
bubble_sort(a)
###########################################################
# 찐또배기 재귀함수
a=[5,4,3,2,1,8,7,10]
def recur_bubble(a,i=1,b=[]):
if i==len(a)-1: # 최대 범위 도달 시 다시 처음으로
b.insert(0,a.pop())
recur_bubble(a,1,b)
else:
if len(a)==1: # 길이가 1이면 정렬 완료
print('정렬 완료')
b.insert(0,a.pop())
print(b)
return b
elif a[i-1]>a[i]: # 길이가 1이 아니고, 순서가 다르면
a.insert(i-1,a.pop(i))
recur_bubble(a,i+1,b)
else: # 길이가 1이 아니고 , 순서가 맞으면
recur_bubble(a,i+1,b)
recur_bubble(a)
while 문으로 풀려고 고생했는데 고생해봤자였다. 어차피 데이터가 10000개 이상이 되면 둘 다 더럽게 느리다!
버블 정렬 너무 구식이야.. ㅠ
'코딩 > 문제' 카테고리의 다른 글
| 문제6. (파이썬) 합병정렬 (0) | 2020.06.05 |
|---|---|
| 문제5. (파이썬) 삽입정렬 (0) | 2020.06.04 |
| 문제3. (파이썬) 이진탐색 (0) | 2020.06.02 |
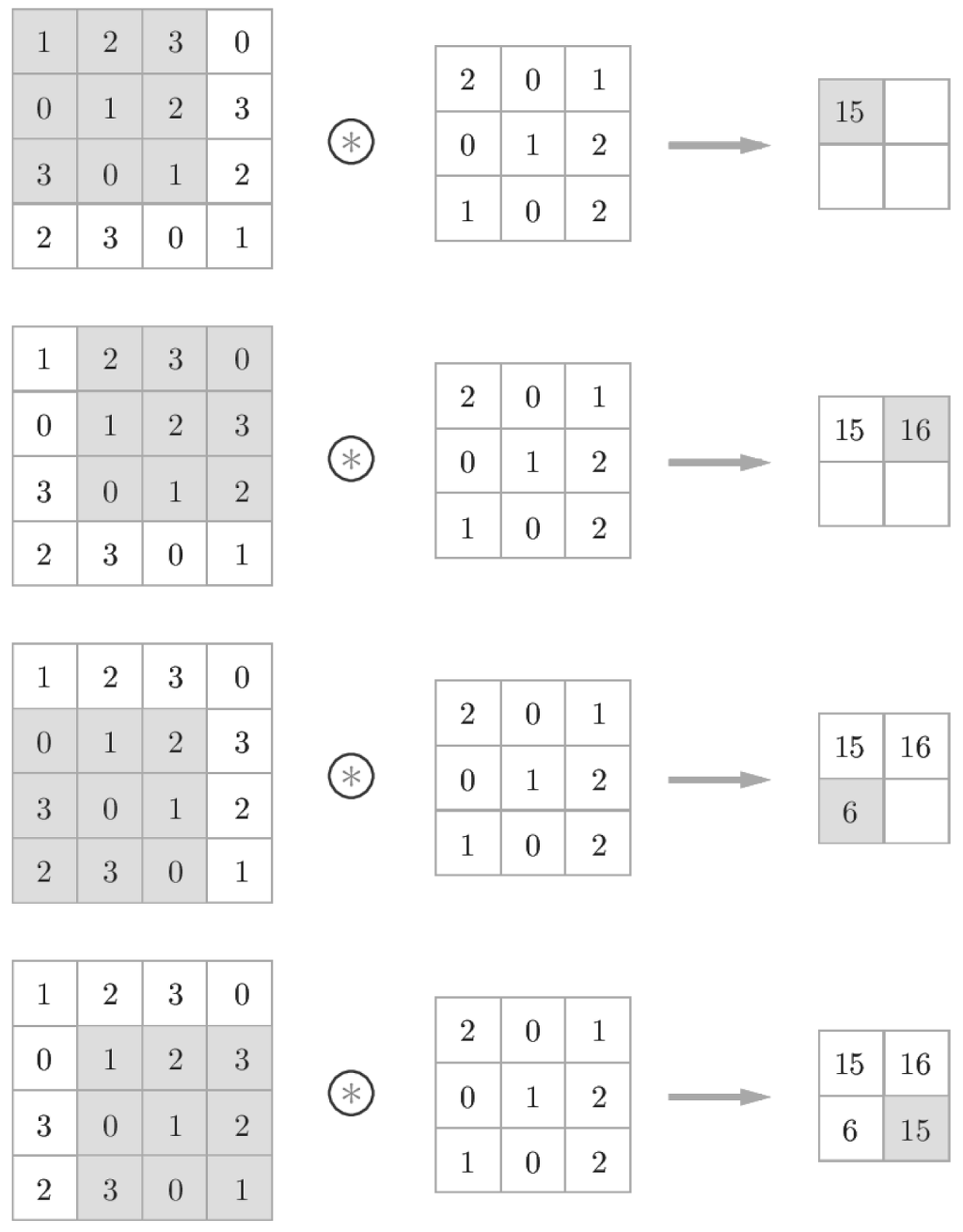
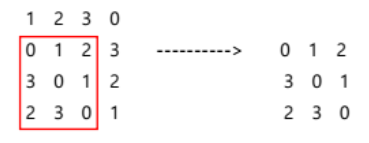
| 문제2. (파이썬) matrix_convolution 구현 (0) | 2020.06.01 |
| 문제1. (파이썬) np.dot을 for문으로 구현하기 (0) | 2020.05.15 |